正方形直角证明三角形全等，数学三角形例题详解

正方形的特殊之处

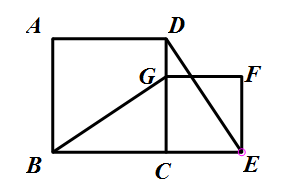
都知道正方形有4条等边，4个等角都是90°，对于证全等三角形来讲，已经有了1对等边和1对等角，我们只要再找1对角或1对边就能证全等。比如下面的图，我们很容易证明，△BCG≌DCE。

例题一：

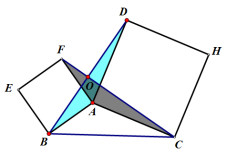
ABEF和ACHD均为正方形，证明：（1）、BD⊥CF （2）、BD=CF

解题思路：

要证明（1）和（2），其实只要证明△BAD≌△FAC就行。因为2个正方形，可以得到BA=FA,AD=AC,还差一夹角。

而∠BAD=90°+∠FAD,∠FAC=90°+∠FAD,利用了正方形的直角，很容易得到∠BAD=∠FAC，那么△BAD≌△FAC也就有了。所以BD=CF

因为全等，∠BDA=∠FCA，而∠BDA+∠BOC+对顶角=∠FCA+90°+对顶角=180°，所以∠BOC=90°，也就是BD⊥CF。

总结：此例题很好的利用了正方形的等边，直角，再通过三角和为180°，找到等角，最后证得全等。

例题二

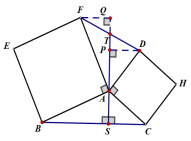
ABEF和ACHD均为正方形，AS⊥BC交FD于T，求证：T为FD的中点

解题思路：

T为FD的中点，也就是证FT=TD,那么我们就要想到找这两条边相关的三角形，是否全等，看图似乎找不到，那就作辅助线。很自然想到，延长SA，因为题中数不清的直角，所以我们优先想到在SA上和SA的延长线上做垂线。所以过F作SA的延长线的垂线，垂足为Q,过D作ST的垂线，垂足为P。

然后很容易知道，△FQT和△DPT有三对角相等，这时候我们需要一对边来证全等。

有过例一的练习，很容易证△FAQ≌△ABS，所以FQ=AS，同理，△DPA≌△ASC,所以DP=AS,所以得到另一对等边，FQ=DP,然后根据AAS证得△FAQ≌△ABS，那么T为FD的中点也可得到。

例题三

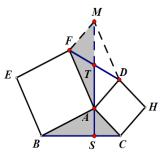
ABEF和ACHD均为正方形，M为FD的中点，求证：AS⊥BC

要证AN⊥BC，也就是证明直角。∠FAQ+∠BAS=90°很容易知道，所以只要得到∠SBA+∠BAS=90°就可以证明AN⊥BC。

先用例2的辅助线，看能不能解决问题。想办法证明△FAQ≌△ABS，但是只能找到一对等边，无法证明∠FAQ=∠ABS，所以此路不通。

T是中点，也就是FT=TD,那么找与这两条边有关的全等三角形这个想法不变，既然作垂线不能多出一对等角，无法证明全等，那么不妨造一对等边，看看会不会出现全等。所以尝试，延长AT到M,AT=MT,连接FM,DM

我们很容易知道四边形MFAD是平行四边形，因为对角线平分的四边形是平行四边形。FM=AD=AC,而AB=AF,要证△MFA≌△CAB，只要再找一个夹角就行。那么∠MFA=∠CAB吗？

∠CAB+∠FAD=360°-90°-90°=180°,FM//AD可得∠FMA+∠FAD=180°,示意图∠CAB=∠MFA，一对等角有了，然后根据SAS证明全等，然后角和90°很容易得到∠ASB=90°。

总结

例二和例三条件和结论的互相证明，很好的体现了正方形等边、直角的好处。通过90°和180°不断找寻角和角的关系，最后证全等。通过这3个例题，以后看到正方形，应该知道怎么去找全等三角形了。