角平分线构造全等三角形（数学三角形解题技巧）

通过角平分线构造全等三角形的原由

要证三角形全等，就要满足SSS，SAS，AAS和SAS，而角平分线可以得到一对角相等以及一条公共边，那么只要在找一条边就可以有全等，也就是说，有了角平分线，就容易得到全等三角形。

如何构造全等三角形

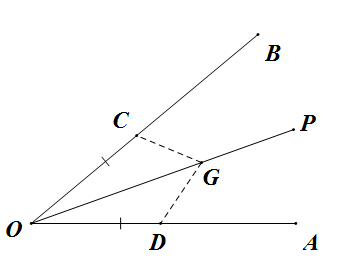
方法一：找一对边，即OC=OD,那么根据SAS易证△COG≌△DOG，

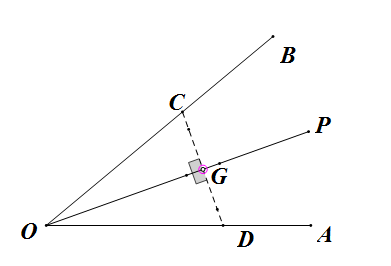
方法二：找一对角，往往是直角，因为直角容易做。比如OP上找一点G,过G做OP的垂线，交OB于点C，交OA于点D，那么∠OGC=∠OGD，然后根据ASA易证△COG≌△DOG

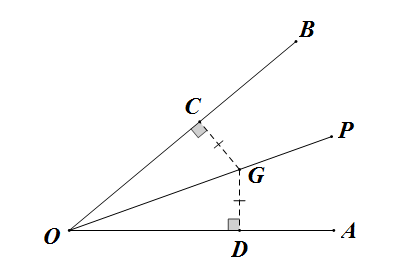
方法三：根据角平分线的性质，角平分线上的点到角两边的距离相等。过点G做OB的垂线交于点C，做OA的垂线交于点D，CG=DG，可以根据HL（斜边和一条直角边对应相等的两个直角三角形全等），证△COG≌△DOG，也可以根据AAS证全等。

练习题一

如图，△ABC的角平分线AD与BE交于点I，求证：点I在∠ACB的平分线上．

解题思路：

这个题其实就是在证明，三角形的角平分线交于一点。

所以，作IH⊥AB，IG⊥AC，IF⊥BC，AD平分∠BAC，可得两角相等，通过AAS可证△AHI≌△AGI，可得IH=IG，同理可得IH=IF，所以IF=IG（等量代换）

然后连接，IC，△IFC和△IGC是直角三角形，根据HL就可以证明△IFC≌△IGC,可得∠ICA=∠ICB,也就是点I在∠ACB的平分线上

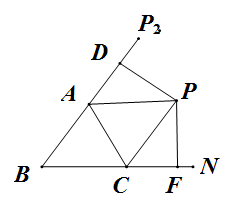
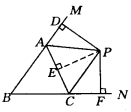
练习题二

PA、PC分别是△ABC外角∠MAC和∠NCA的平分线，它们交于点P，PD⊥BM于D，PF⊥BN于F．

求证：BP为∠MBN的平分线．

证明思路：

有角平分线，有垂直，很自然的想到过P作AC的垂线

有角平分线，有垂直，我们很自然想到，做垂线。过点P作AC的垂线，垂足为E，易证△PMA≌△PEA，可得PM=PE。同理可证△PEC≌△DOG，可得PF=PE,所以PM=PF，所以P在BP上。

角平分线的基本性质，点到两边距离相等，点在角平分线上

总结

角平分线的练习题比较少，因为通过角平分线证全等，往往会用到“截长补短法”