初三抛物线方程及图像（数学抛物线的几何性质）

同学们大家好～

今天我们来重点研究一下抛物线有哪些几何性质。

第一，就是根据抛物线的定义一样就能看出来的，抛物线上的点到焦点的距离（焦半径）等于到准线的距离。或者说是，抛物线上点到焦点的距离与到准线的距离的比值为1。我们用一个符号e来表示抛物线上点到焦点的距离与到准线的距离，即e=1。当然它也有一个中文名字，叫做：离心率。

接下来我们来研究抛物线的另一种极重要的性质。昨天我们讲了抛物线的四种标准方程，今天我们来研究其一：y方=2px。

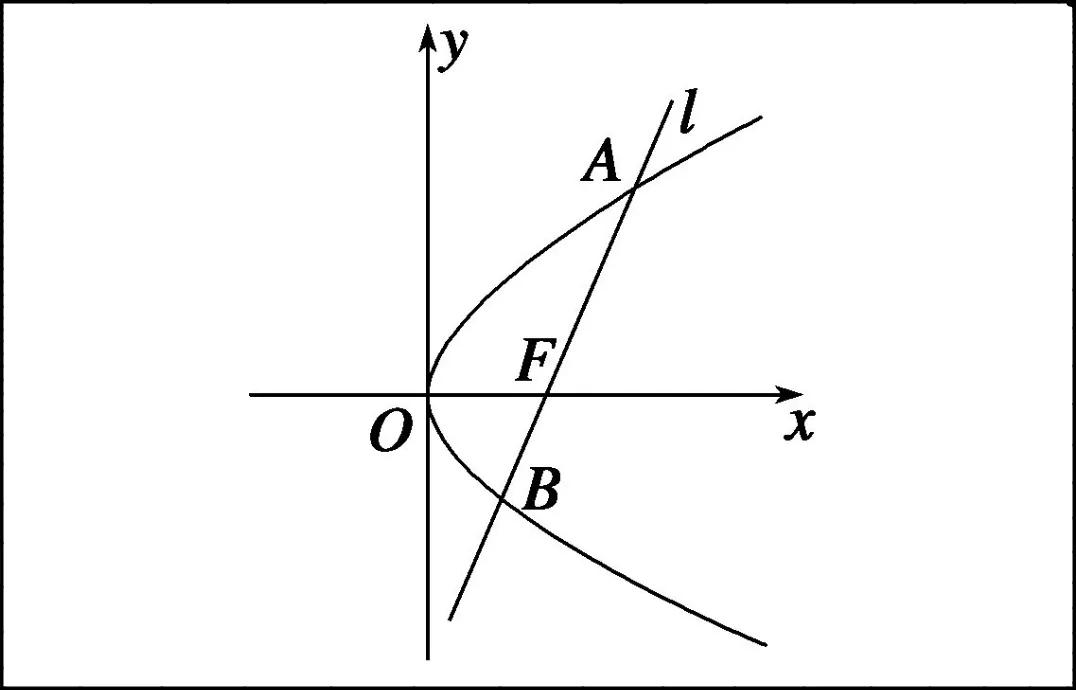
如果我们将这个抛物线上任意两点连接，就会形成一条线段，我们把这条线段成为抛物线的弦。特别的，如果这条弦过焦点，我们就叫焦点弦。如下图‬：

AB即为焦点弦。

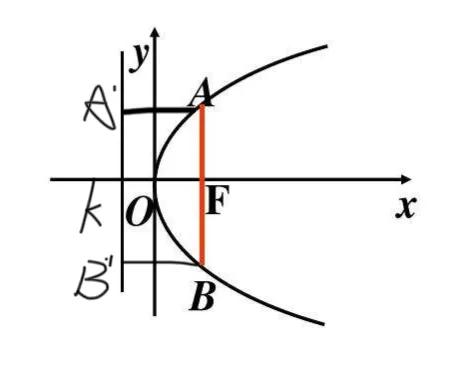
再特别一点，如果这条焦点弦还垂直于对称轴（图中即x轴），我们就叫它通径。如‬下图‬：AB垂直‬于‬x轴‬

AB就是抛物线通径。

那么他们分别具有什么性质呢？我们先来看一级特殊的焦点弦。

取AB中点C，分别过A，B，C作AA’ ,BB‘ ,CC’ 垂直于准线。求证：CA=CB=CC’

提示：需要用到梯形中位线的性质

想到了吗？

等式前半截CA=CB好证，直接利用线段中点定义。但是怎么跟CC’找到联系呢？

根据线段中点定义，我们同时还可以得到CA=CB=1/2AB，那也就是说，要是我们能证明出CC’也等于1/2AB就行了。

而AB作为焦点弦，它由两部分组成：AF和BF（注：抛物线上点与焦点的连线叫做焦半径），焦半径的长是等于那个点到准线的距离的，也就是AF=AA’，BF=BB’，那么AB=AA’+BB’——同时我们还得到一个附属结论。

那么，CC’与（AA’+BB’）有什么关系呢？不难看出，CC’实际上是梯形ABB’A’的中位线，这样就可以得出：CC’=1/2(AA’+BB’)。即CC’=1/2AB=CA=CB。

换句话说，A，B，C’三点共圆，圆心为C。

通径

那我们再来看通径。它不就是垂直于轴的焦点弦嘛。我们主要会计算它的长度就可以了。刚才我们推出的附属结论，通径AB就等于AA’+BB’，但是此时由于位置特殊，AA’和BB’都等于KF，而KF不就是我们标准方程中的p嘛，所以AA’=BB’=KF=p，所以AB=2p。