数学全等三角形专题，截长补短法构造全等三角形

所有证明只有详细思路，没有具体的答题过程，因为做数学题思路高于一切！

如果有错别字，或者其他错误，请及时反馈，我会及时纠正！

截长补短法构造介绍

若遇到证明线段的和差倍分关系时，通常考虑截长补短法，构造全等三角形。

①截长：在较长线段中截取一段等于另两条中的一条，然后证明剩下部分等于另一条；

②补短：将一条较短线段延长，延长部分等于另一条较短线段，然后证明新线段等于较长线段；或延长一条较短线段等于较长线段，然后证明延长部分等于另一条较短线段

截长补短法构造全等——例题一

在四边形ABCD中，BC＞AB，AD=DC，BD平分∠ABC.求证：∠BAD+∠BCD=180°

要证∠BAD+∠BCD=180°，想办法把这两个角整到一起，比如同在三角形中，或者同在一条直线上。

在BC线段上截取BE，连接DE，这样∠BAD和∠BCD就有办法联系在一起了。

BD平分∠ABC.+公共边+等边（SAS）可以证得△ABD≌EBD，得∠BAD = ∠BED,AD=DE

因为AD=DC，可得△DEC是等腰三角形，即∠DEC = ∠BCD。

∠BED+∠DEC=180°,很自然得到∠BAD+∠BCD=180°

截长补短法构造全等——例题二

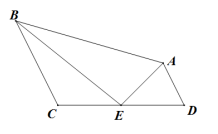
如图，AD∥BC，EA,EB分别平分∠DAB,∠CBA，CD过点E，求证;AB＝AD+BC。

证明思路：

方法一：通过“截长”构造全等

AB截取线段AF，使AF=AD。

AF=AD + EA平分∠DAB + AE公共边，易证△AEF≌AED（SAS），可得AF=AD,∠AFE=∠D

AD//BC可得∠D+∠C=180°,∠BFE+∠AFE = ∠BFE+∠D=180°,可得∠BFE=∠C

然后根据AAS易证明△FBE≌CBE,可得FB=BC，最后得出AB=AF+FB=AD+BC

方法二：通过“补短”构造全等

延长BC到G，使CG=AD。

根据SAS易证△ABE≌GBE,得AB=BG，∠BAE=∠G

AE平分∠BAD,可得∠BAE=∠EAD,所以∠EAD=∠G,AD//BC可得∠D=∠ECG

2个角1个边，就可以通过ASS证明△ADE≌GCE,可得AD=CG

最后可得，AB=BG=BC+CG=AD+BC

截长补短法构造全等——例题三

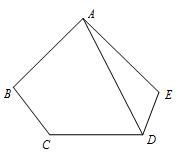
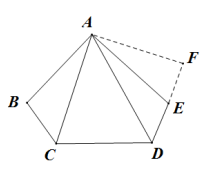
五边形ABCDE中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：AD平分∠CDE

证明思路：

BC+DE=CD，要利用这个条件，得想办法把它们整到一条线或者同个三角形中。∠ABC+∠AED=180°，平角和是180°，三角形和是180°（需要3只角）。所以很自然相到延长DE或者CB，把所有条件整到一条线上去。

延长DE到F，使EF=BC，连接AF。

观察△ACD和△AFD,AD公共边，CD=DE+EE=DF，两边已在，只要再有1边或者1夹角就有全等。但是角相等是要我们证明的，所以找AB=AF。

而AB=AE，BC=EF，∠ABC+∠AED=180°，∠AEF+∠AED=180°（平角和），自然可得∠ABC=∠AEF，根据SAS可以证明△ABC≌△AEF,可得AB=AF

最后根据SSS证明△ACD≌△AFD，∠ADC=∠ADE，也就是AD平分∠CDE

截长补短法构造全等——例题四

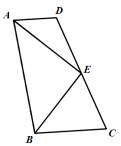
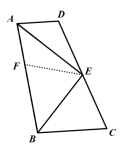
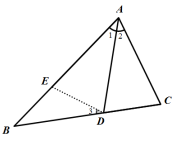
已知四边形ABCD中，AD//BC，若∠DAB的平分线AE交CD于E，连结BE，且BE恰好平分∠ABC，判断AB的长与AD＋BC的大小关系并证明.

要比较AB和AD＋BC的大小关系，就要把三条边整到同个三角形或者同一条线上。很自然想到“截长补短”。“补”很难找到全等三角形，那就"截"。

线段AB上做BF=BC，连接EF

解题思路：

BF=BC+BE平分得角相等 + BE为公共边可得△BCE≌△BFE，可得∠BFE=∠BCE

AD//BC可得∠D+∠BCE=180°,而∠AFE+∠BFE=180°（平角和），所以∠AFE=∠D

AE平分∠DAB，可得∠FAE=∠DAE，根据AAS可得△FAE≌△DAE，可得AF=AD

最后，AB=BF+AF=BC+AD

截长补短法构造全等——例题五

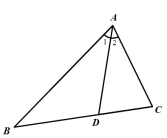
△ABC中，∠C＝2∠B，∠1＝∠2。求证：AB＝AC＋CD．

很自然想到“截长”，在AB上取AE=AC。

易证△AED≌△ACD,可得AE=AC，∠AED=∠C

因为∠AED=∠B+∠3，所以∠C=∠B+∠3，因为∠C＝2∠B，所以∠B＝∠3,可得EB=ED

最后，AB＝AE+BE=AC+CD

总结：

截长、补短的目的就是把线段整到同一条线上或者同一个三角形中。然后根据三角形和直线的一些性质解题。