
求四边形的外接圆半径(高中几何题解题思路)
ashao
04-23 15:31
1396 阅读
我爱育娃
一道高中几何题-求圆内接四边形的外接圆的半径 一个圆的内接四边形的相连的四个边分别是25, 39, 52, 60,求这个圆的直径。 解: 如图, 设AB=25, BC=39, CD=52, DA=60,∠DAB=y, 并设D
一道高中几何题-求圆内接四边形的外接圆的半径
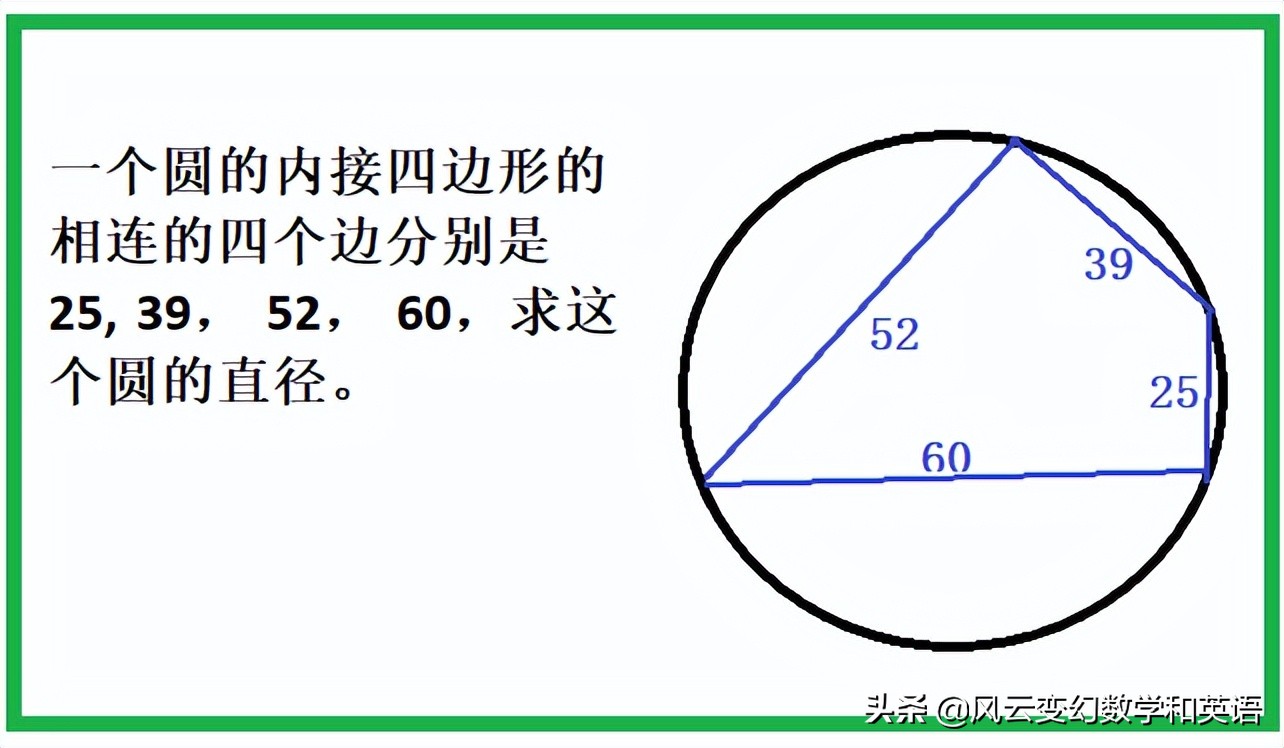
一个圆的内接四边形的相连的四个边分别是25, 39, 52, 60,求这个圆的直径。
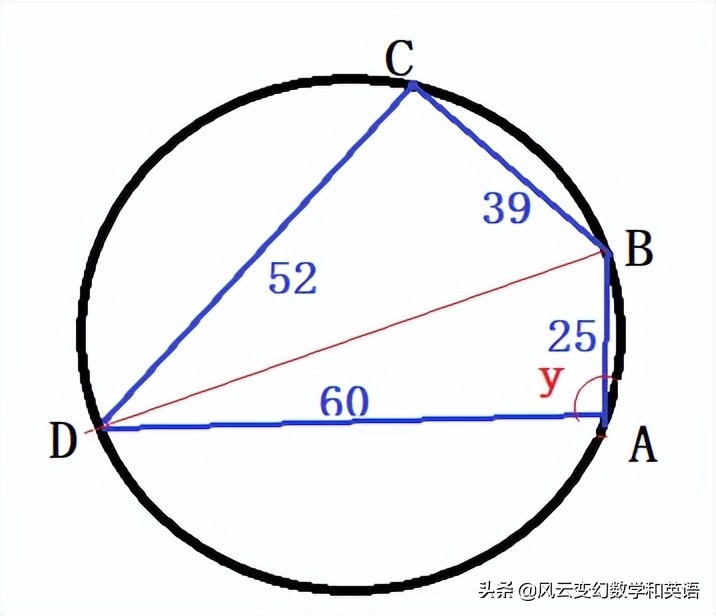
解: 如图, 设AB=25, BC=39, CD=52, DA=60,∠DAB=y, 并设DB=x,
在三角形DCB和三角形DAB中分别用余弦定理:
由于:
化简:
由此可以推出:
cos(y)=0,
即y=90°
因此DB是直径, 利用勾股定理可以得出:
实际上另一种解题思路是,当发现:
就发现了BD是直径,这是因为只有对应的四边形的对顶角为90度才有此结果。这一点通过上面的推导过程可以证明, 读者自己可以确认。
思考,此题恰巧赶上了对角的余弦是0, 若假定没有cosy=0的情况,这道题也是可以求解的,因为通过cosy的值可以算出siny, 同样可以通过三边长度求出另一个角的余弦,再算出正弦,这样通过正弦定理就可以直径, 因为:
a/sinA=b/sin B=c/sinC=2R
- 上一篇:斜面的机械效率公式,初中物理简单机械考点汇总
- 下一篇:没有了
相关文章
文章评论
求四边形的外接圆半径(高中几何题解题思路)文章写得不错,值得赞赏
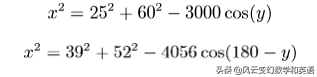
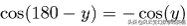
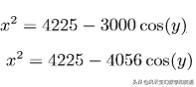
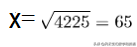
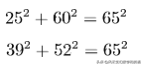


 微信收款码
微信收款码 支付宝收款码
支付宝收款码