高中关于求一元函数值域怎么解（精选习题详解说明）

【分析】这是一道求一元函数值域的问题，值域是函数自变量取遍定义域内的每一个值所对应的函数值的集合，求函数值域的通法是利用求导的方法，利用函数的单调性求出函数的最值，进而得到值域。如果观察到这个函数解析式的结构特征，即其分式的分子与分母是齐次的特点，不用求导，而是用初等方法就可以解决。由于分母x-1是多项式，若直接将其放到根号内，变形后的表达式较为复杂，这时，我们利用函数值域的定义，再结合值域的几何特征，发现图像的左右平移并不改变函数的值域，利用函数值域的平移不变性，由于函数y=f（x）与函数y=f（x+1）的值域相同，问题转化为求函数 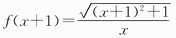 的值域问题了。显然，这样的转换的好处在于可将其分母x-1化为单项式x，大大简化了代数变形的难度。简解如下：



 

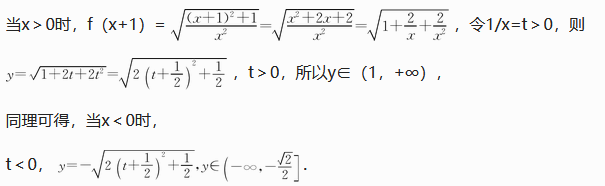
通过对本题的解决，加深了对函数值域的理解，特别是从“形”的角度的理解，即函数值域就是函数图象在y轴上“投影”所覆盖的区域的范围，这就是解决此问题的价值所在。如果有了这样的理解，再遇到类似问题，我们就能够找到更好的方法了。例如，已知函数f（x）=x 2 +ax+b的值域为[0，+∞），且不等式f（x）＜c的解集为（m,m+6），求c的值。这样的问题，我们就能看出答案了。或许，在有些人的眼里，这叫做解题“技巧”，但实际上，只是对数学概念的理解更深一些罢了。

（二）通过解题梳理一类问题的通法

如果就题解题，数学有永远也解不完的题目，进而陷入“题海”，如果能从一道问题的解法中，通过梳理，获得一类问题的“通法”，就有可能跳出题海。