高中数学函数零点的定义（函数的零点含义及例题）

一、函数的零点：

1、定义：一般地，如果函数 y = f ( x ) 在实数 a 处的值等于零 f ( a ) = 0 ，则 a 叫做这个函数的零点。

对于任意函数，只要它的图像是连续不间断的，其函数的零点具有下列性质：

① 当它通过零点（不是偶次零点）时函数值变号；

② 相邻两个零点之间的所有的所有函数值保持同号。

2、函数零点个数的确定方法：

① 判断二次函数的零点个数一般由判别式的情况完成；

② 对于二次函数在某个闭区间上零点的个数以及不能用判别式判断的二次函数的零点，则要结合二次函数的图像进行；

③ 对于一般函数零点的个数的判断问题不仅要在闭区间 [a , b] 上是连续不间断的，且f(a) ·f（b）＜0，还必须结合函数的图像和性质才能确定。

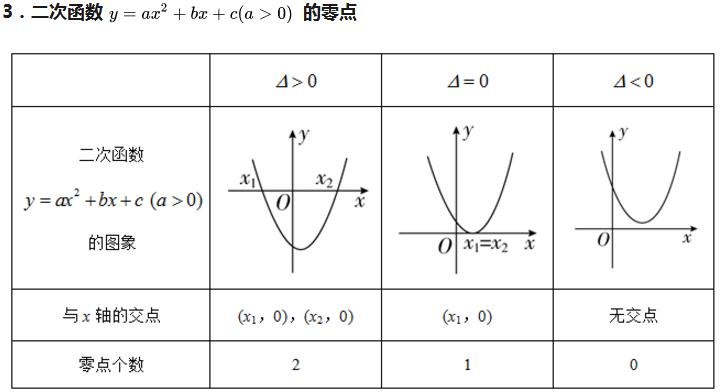
函数有多少个零点就是其对应的方程有多少个实数解。

二、典型例题

1、求函数的零点

例题1、求函数 y＝x^3－x^2－4x＋4 的零点 。

答案：－2 , 1 , 2 。

2、零点个数的判断

例题2、判断函数f(x)＝x^2－7x＋12的零点个数 。

解： 由 f(x)＝0，即 x^2－7x＋12＝0 得 Δ＝49－4×12＝1 > 0，

∴ 方程 x^2－7x＋12＝0 有两个不相等的实数根 3, 4，

∴ 函数 f(x) 有两个零点，分别是3 , 4 。

3、函数零点的应用

例题3、若关于x的方程x^2＋(k－2)x＋2k－1＝0 的两实数根中，一根在0和1之间，另一根在1和2之间，求实数 k 的取值范围。

解：设函数 f(x)＝x^2＋(k－2)x＋2k－1，先画出函数的简图，如下图所示；

函数 f(x)＝x^2＋(k－2)x＋2k－1的图象开口向上，零点x1∈(0,1)，x2∈(1,2)。

例题3图（1）

由 ： f ( 0 ) > 0 , 得 2k - 1 > 0 ； f ( 1 ) < 0 , 得 1 + k -2 + 2k - 1 < 0 ； f ( 2) > 0 , 得 4 + 2(k - 2) + 2k - 1 > 0 ；

解得：1/2 < K < 2/3 ∴ 实数 k 的取值范围是 [ 1/2 , 2/3 ] 。

三、拓展提高

1、已知 f(x) 是定义在R上的奇函数，当 x ≥ 0 时，f(x)＝x^2－3x, 则函数g(x)＝f(x)－x＋3的零点的集合为 ( D )

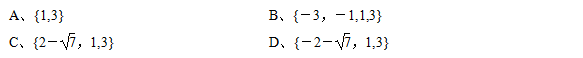
第1题图

2、已知 x＝－1是函数 f(x)＝a/x ＋b (a≠0) 的一个零点，则函数 g(x)＝ax^2－bx 的零点是 ( C )

A、－1 或 1 B、0 或－1 C、1 或 0 D、2 或 1

3、三次方程x^3＋x^2－2x－1＝0 的根不可能所在的区间为 ( C )

A、(－2，-1) B、(－1,0) C、(0,1) D、(1,2)

4、若函数 f(x) 在定义域 {x|x≠0} 上是偶函数，且在(0，＋∞)上是减函数，f(2)＝0，则函数f(x)的零点有( B )

A、一个 B、两个 C、至少两个 D、无法判断

5、若关于 x 的方程ax^2＋bx＋c＝0(a≠0)有两个实根1、2，则函数 f(x)＝cx^2＋bx＋a 的零点为( C )

A、1 , 2 B、－1，－2 C、 1，1/2 D、－1，－1/2

6、已知函数f(x)＝ax^3－2ax＋3a－4 在区间 (－1,1) 上有一个零点 ，求实数 a 的取值范围 。

答案：1 < a < 2 。